10/8/20
A popular narrative explaining the outcome of the 2016 election is Hilary Clinton was just unlucky. On election night, the odds were in her favor, but when the dice were cast she unfortunately rolled snake eyes. In a weird way, if the election were just run another day, she would win.
The underlying assumption is that elections are sort of random. But, how similar is winning an election to playing roulette? Let’s briefly relate what actually happens on voting day. People who want to vote, visit a voting location. They select a name either by pushing a button or writing it in. Later, the votes are tallied and grouped by region and a winner is announced. Where is the randomness? At each step of the process it’s simple cause and effect.
An individual might have an unexpected accident, preventing them from voting, but like most other days, the vast majority of the population is able to carry out their intentions. It’s even difficult to detect rapidly changing variables which might appear random. The cultural and economic context have been slowly evolving over years. The media environment has been built up over months leading up to it. Individual’s political views move slowly, as they are predominantly a product of deeply rooted influences, including family upbringing, income, ethnicity, religion, and education.
If the unlucky dice roll doesn’t hold up to a little scrutiny, then why is this view so popular? Perhaps it is because its message avoids uncomfortable conclusions. If it was just bad lack, then it was nobody’s fault. We still have the popular ides. It’s not even clear that our strategy must change to win next time. The alternatives are much harder to look at.
Hold on a minute. Perhaps this is all a misunderstanding. People don’t actually believe elections function like a lottery. When journalists use percentages they are just referring to the confidence intervals of polls. Pollsters want to survey public opinion. But, they can’t talk to everyone in the country, so they talk to a sample, and then use probability to guess how likely it is that this sample represents the whole population. It’s basic statistics (as described in this Pew Research article).
This may correctly describe where the numbers come from. Perhaps in a back office somewhere, there actually is a Ph.D in Stats coolly scrutinizing surveying models. But this is clearly not how these figures are interpreted by journalists and otherwise intelligent or scientific people. If it was, they would be concerned with potential gaps between sample and population, instead of calculating their odds. Look at how randomness and chance is implied in the following popular media:
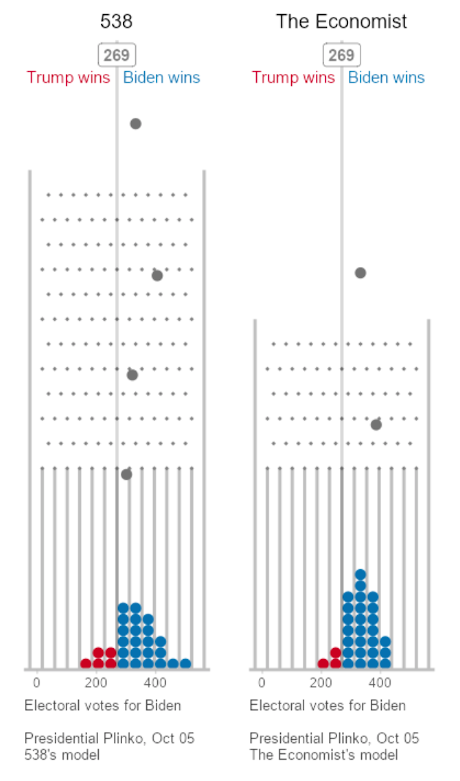
Election as a Pachinko/Plinko Machine
From: presidential-plinko.com, a site created by a Northwestern University professor.

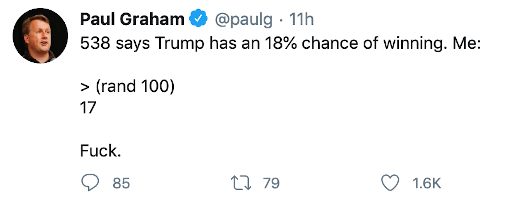
Election as an Unlucky Dice Roll
From Paul Graham’s Twitter, a popular figure in tech and startups.
20% is still 1 in 5
A comment on the Silicon Valley forum “Hacker News”.

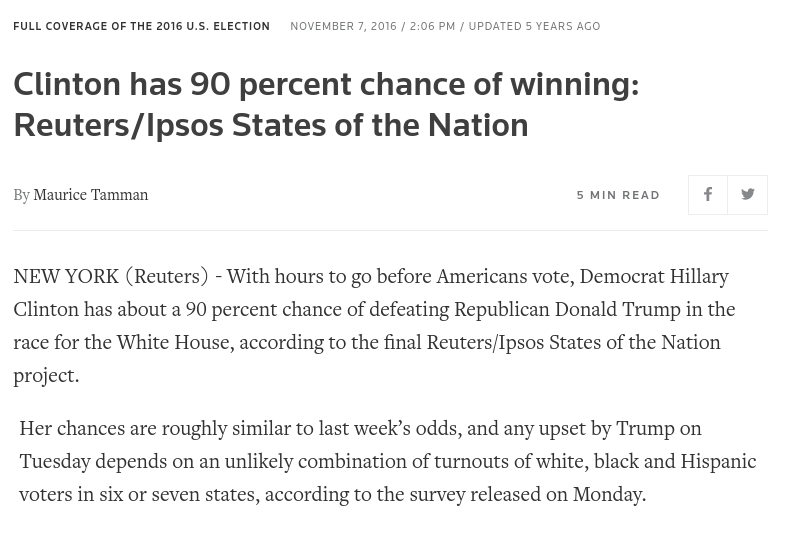
The unlikely combination
From Reuters.
If so many smart people are doing inappropriate probabilistic thinking in this area, are there others where we might be making similar mistakes?
Stats is at the forefront of business, marketing, medicine, sports, finance, academia, and science. Many of it’s concrete applications are no doubt useful and appropriate. But, our society’s interest in it goes well beyond it’s technical or economic usefulness. Its popularity is partially an extension of our love for science and logic. Just look at all the numbers, equations, and graphs! But, that also isn’t enough to explain its significance. Consider the following ideas prominent in popular culture:
If we apply the same step-by-step analysis as we did with the election, these ideas immediately begin to seem less plausible, or at least in need of some qualification and refinement. Perhaps the cultural prevalence of randomness nudges us to reach for that option more often than alternatives. Contributing to this bias is the fact that randomness can provide us with comfortable answers to hard questions, or mask the fact that the underlying mechanisms are not well understood.
Let’s step back a bit. Probability itself is a sound mathematical model. Just because an underlying process is not random, does not mean that probability cannot offer an accurate description or be a useful tool. Sometimes statistics is the best way to talk about complicated deterministic systems.
For example, statistics can be used in physics to describe the motion of bodies, which can otherwise be accurately described by deterministic cause and effect. A gas might be modeled as a cloud of individual particles, each of which is well understood, but there may just be too many of them to keep track of. Because, the task is overwhelming, and we care most about the global behavior, we settle for partial information (see Wikipedia).
Consider even a dice roll. With Newtonian mechanics we can understand gravity, the force of the throw, the friction in the air, the impact on the table, and with all this make an accurate prediction of the outcome. But no human can capture all those parameters in a split second and apply them. Without a controlled environment for study, probability is a good model.
Computers despite being artificially deterministic, benefit greatly from probability. Random numbers generated on a computer are usually just functions which are difficult to predict. Despite this, they can compute and solve problems using probability (see Monte Carlo methods).
The difference then between helpful and misleading attributions of randomness, is of course how closely the model actually resembles reality. Statistical models in physics don’t just start by assuming processes are random. They construct deterministic relationships between the elements; the energy, the area, the force, and then insert a tiny amount of probability to account for the arts that are too complex. The random processes are tightly constrained by the physical laws. Furthermore, they can usually quantify the information lost by assuming randomness.
It may seem like the only conclusion we can draw is, “lazily constructed models give poor results”. But, this analysis also reveals how backwards common statistical practices is. Statistics is the go-to tool when we have no ideas what’s going on. Fields like politics, financial markets, and human behavior come to mind. Instead of starting with well understood systems and then carefully relaxing assumptions and summarizing details, Data is automatically correlated, and everything is basically assumed to follow random distributions. Randomness replaces cause and effect, instead of working in concert with it.
The sophistication of the math involved, disguises all this. But, is it any surprise that we observe “black swan” events when we assume everything uniformly follows a bell curve?
In The Republic X, Plato observes a related attitude in painting and poetry:
The imitator, I said, is a long way off the truth, and can do all things because he lightly touches on a small part of them, and that part an image. For example: A painter will paint a cobbler, carpenter, or any other artist, though he knows nothing of their arts; and, if he is a good artist, he may deceive children or simple persons, when he shows them his picture of a carpenter from a distance, and they will fancy that they are looking at a real carpenter.
And whenever any one informs us that he has found a man knows all the arts, and all things else that anybody knows […] I think that we can only imagine to be a simple creature who is likely to have been deceived by some wizard or actor whom he met, and whom he thought all-knowing, because he himself was unable to analyze the nature of knowledge and ignorance and imitation.
And so, when we hear persons saying that the tragedians, and Homer, who is at their head, know all the arts and all things human, virtue as well as vice, and divine things too, for that the good poet cannot compose well unless he knows his subject, and that he who has not this knowledge can never be a poet, we ought to consider whether here also there may not be a similar illusion. Perhaps they may have come across imitators and been deceived by them
Statistics students and professionals hold the same remarkable belief about their own field today. They don’t need to study any subject or “applications”, besides statistics itself. Their statistical knowledge is immediately transferable to understanding any problem thrown their way. It’s a universal framework for understanding. This makes it the perfect career in the culture of randomness, and ironically minimize the need to make predictions about the future.
But can you understand business without running one? Can you understand voting patterns without understanding what is happening in people’s lives? Can you understand psychology without thinking, observing, and talking to people? In these areas, as in politics, we can conclude that probability and statistics are being used as poor substitutes for explanatory theory.
Update 09/25/2021: Heavily edited the second half to clarify intended message. The election discussion is largely the same.